Tower of Hanoi

 

The Tower of Hanoi is a puzzle whose goal is to move all the disks from one post to another post by only moving one disk at a time and never placing a larger disk on top of a smaller disk. Our department has two of these games to take to the classroom.

 

 

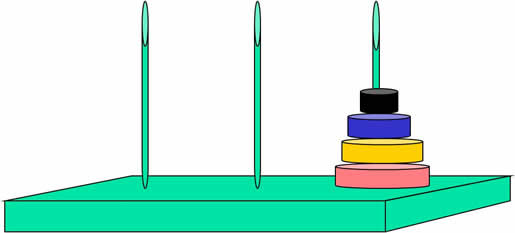
Suppose that only one disk is on a spike. How many moves are required? Count it.

 

 

Only 1 move

 

 

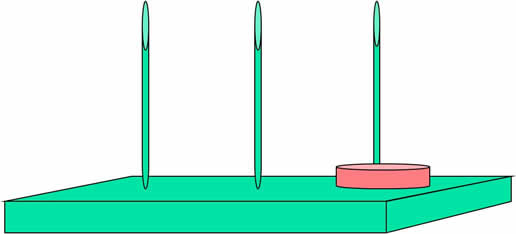
Suppose that two disks are on one spike. How many moves are required? Count them.

 

 

Only 3 moves

 

 

Suppose that three disks are on one spike. How many moves are required? Prediction?

 

 

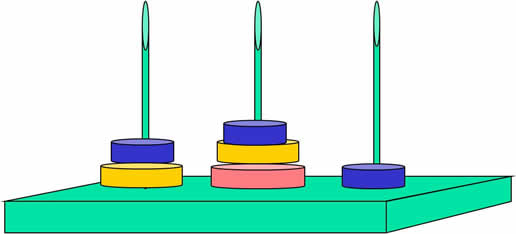
Only 7 moves

 

 

What is the pattern?

 

 

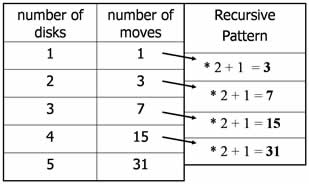
Extend this recursive process until the number of disks reaches 64. You can use the calculator with the following commands:

 

1 enter	for the first number of moves
ANS*2+1 enter	to get the second number of moves
enter	62 times to reach 64 disks to obtain 1.8446744 X 1019 moves

 

This iterative process is said to define a sequence RECURSIVELY. Using the notation a₁ , a₂ , a₃ , … , a_n , a_n+1 , … , we can write the sequence with the formulas:

 

 

 

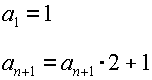
The recursive formula can also be written in terms of the number of disks:

 

 

This pattern generalizes to a formula that can be used to find the number of moves needed when using 64 disks. Using sequence notation, the GENERAL TERM FORMULA (also called the nth term) is written as:

 

 

So, 2⁶⁴ – 1 equals 1.8446744 X 10¹⁹ moves.