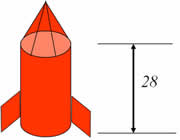
Rocket Design

 

A rocket consists of a right circular cylinder of height 28 meters surmounted by a cone whose diameter is equal to its height. Determine the radius of the rocket if it is to have a total volume of 1000 cubic meters.

 

 

The volume of the cylinder section is

The volume of the cone section is

Summing the two volumes results in a cubic polynomial for the total volume.

We want a rocket volume of 1000 cubic meters, so we need to solve for r when V = 1000. Putting in this value and subtracting 1000 from both sides gives

Our knowledge of cubic polynomials implies that we either have 1 real solution and 2 complex solutions or 3 real solutions where we will need to determine which of the 3 solutions is best. Graphing the right side of the equation to determine the real zeros will give the radius of the cone section that produces a total volume of 1000.

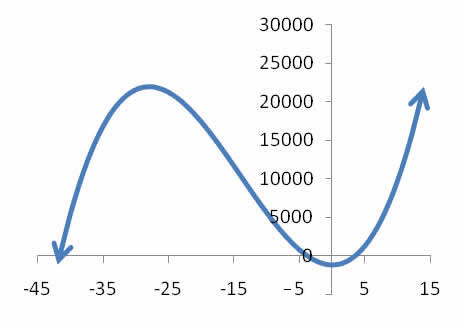
The only positive real zero is 3.2484, so a radius of 3.2484 meters is needed on the rocket. (Two negative zeros also exist, however they are not relevant to this application.)