Chapter 5 

Assessment of Student Learning

Assessment is a comprehensive process with many facets.  This chapter focuses exclusively on assessment ofstudent learning of mathematics, one of the most important professional responsibilities of mathematics faculty andone that should be as much a part of the faculty role as teaching classes.(1)  Assessment, because it involves evaluating student performance, extends beyond assigning grades.  While grades are important, they do not always tell us exactly what students know and can do.  Two students who receive the same grade may not know the same concepts or have the same skills.  Grades may be a way to rank students’ achievement, but are not indicators of specific knowledge or abilities. Standards for grading may differ with each instructor.(2)  Thus, grades do not generally provide the necessary information to make needed changes in pedagogy, curriculum, prerequisites, or other aspects of courses or programs.

Assessment of student learning is a process of helping mathematics faculty adapt instruction to the needs of students.  Assessment provides the mathematics department with information to make informed decisions about course content.  It is alsothe process by which a college assesses what mathematics students know at the end of a student’s course or program.  Assessment is an ongoing activity that leads to improvement in student learning by providing data necessary for making informed decisions at the class, course, and program levels. 

The Assessment Cycle

Assessment is a cycle that begins with a statement of desired student learning outcomes.  The Implementation Cycle presented in Chapter 3 is easily adapted to the assessment of student learning in Figure 2 on the next page.  The first step involves defining learning outcomes, clear statements of what students will know and be able to do after they have finished a class, course, or program.(3)  Learning outcomes in classes, courses, and programs should reflect the skills, knowledge, and ways of thinking the mathematics department believes are important for students to learn.  Assessment efforts should not be limited to what is easy to measure.(4) 

In step 2, tools are designed to assess student learning relative to the stated outcome.  Assessment must be tied to specific learning outcomes in order to be effective.  A standard is established against which each outcome will be judged. For example, if an outcome requires students to communicate their mathematical thinking, assessment tasks that require written explanations or verbal presentations may be appropriate. 

In steps 3-5 , the assessment tool is implemented and data are collected and analyzed using the established criteria for each learning outcome.  Gaps between desired and actual results are identified and discussed among mathematics faculty.  This thoughtful discussion about what is most important about student learning in mathematics leads to action plans for improvement in the assessment tool, the learning outcomes, course materials, instructional methods, course prerequisites or other curricular or policy changes. 

Finally in step 6, results are documented and improvements are implemented based on the analysis of the data.  This final step of the cycle is often referred to as the feedback loop.  Then the Assessment Implementation Cycle begins again.

Assessment at Three Levels

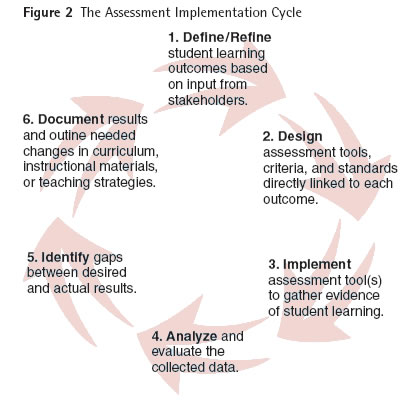
  The assessment cycle provides assurances to students, colleagues, and the external community about the content and quality of mathematics in the first two years of college. Effective assessment includes the documentation of student learning at three levels: class, course, and program. Assessment at each level is the responsibility of all faculty.  It should reflect not only student knowledge of facts and procedures, but also critical thinking and ways of thinking about and communicating mathematics.  When faculty begin an assessment, they should start on a small scale, choosing one or more course or program outcomes to assess.  As faculty gain facility with the assessment process, other learning outcomes can be added to the assessment plan. 

Classroom assessment involves individual instructors assessing individual students’ learning outcomes with instructor-developed tools.  Many assessments are used throughout the term and changed frequently.  Students are informed often about their progress.  Individual faculty who use classroom assessment techniques discover how to adapt instruction to address the learning needs of individual students in a specific mathematics class.  Faculty make frequent and immediate changes to class activities and methods based on assessment results.

Assessment efforts at the course level provide evidence of student learning and motivate changes beyond the individual classroom.  Learning outcomes in individual mathematics classes, in all sections of a particular course, or in sequences of courses or specific programs, are assessed to determine if students are meeting agreed-upon course learning outcomes.  A group of faculty teaching intermediate algebra, for example, can collaborate to discover the instructional strategies or materials best suited to help all students learn the relationship between a quadratic equation and its corresponding graph, an agreed-upon course outcome. 

Assessing outcomes at the program level is the broadest and most overarching form of assessment discussed in this chapter.  Faculty should develop a consensus about the essential student learning outcomes for mathematics courses and programs, as well as the college’s quantitative literacy general education outcomes.  Faculty can use the results of program assessment to determine how all courses in a program, mathematics and nonmathematics courses, help students achieve quantitative goals and objectives.  In addition, external accrediting agencies may have an impact on mathematics outcomes within programs. 

Although classroom assessment should be ongoing, course and program outcomes may be assessed at regular intervals with faculty choosing a different course or program each year.  It is important, however, to complete the assessment cycle for the learning outcomes chosen. In addition to collecting data about many outcomes, improvements should be implemented based on an analysis of that data.  The following table outlines some of the differences in assessment practices at the three levels. 

Table 5.  Multiple Levels of Assessment

Classroom Assessment

Classroom assessment begins with an individual instructor outlining student outcomes for a particular class.  By continuing through the Assessment Cycle and the feedback loop, student progress and growth in mathematics understanding can be assessed, along with mastery of basic skills. Good teachers have always monitored student learning, but assessment makes this monitoring more systematic.(5)  Students are observed in the process of learning by collecting frequent feedback on what, how much, and how well they are learning. In addition to enhancing students’ learning, classroom assessments positively affect students’ perceptions and attitudes about the learning process.(6)  Individual instructors can test assumptions and impressions by checking them against student performance before the student completes the class and can make adjustments before the end of the term.  “When classroom assessment is fully integrated into a course, ongoing assessment becomes part of the faculty member’s overall plan for instruction.”(7)

Classroom assessments, often unique to an individual instructor, are activities that are integrated into instruction and administered during a lesson or class. These assessments may or may not be used for grading purposes, and provide both the instructor and the student with valuable feedback about each student’s progress relative to the learning outcomes.  Student demonstrations to the class, discovery-oriented activities performed in groups, one-minute papers, or other classroom assessment techniques may be included. Assessment that enhances mathematics learning should become a routine part of ongoing classroom activity and should not be viewed as an interruption.(8)  In this way, assessment is not a single event, but integrated with teaching and learning. 

Classroom assessment can have a positive impact on student behavior and performance when it focuses on improving the learning experience, not on identifying individual student weakness.  The assessments may be anonymous and results may be analyzed in the aggregate. Sharing assessment data in class can be an effective learning exercise. (9)  For example, a statistics class might analyze student responses to a brief in-class survey or error patterns in a problem set, then discuss what kinds of improvements might be made.  Student self-assessment can provide an opportunity for students to reflect upon their responsibility for their own learning.  When faculty respond to assessment results by sharing their reasons for changes in instruction, student motivation is increased.  Students realize faculty are interested in their success as learners. 

Classroom assessments can enhance student performance by requiring students to participate actively, reinforcing their grasp of course material, and participating in their own self-assessment. The results are used immediately to redirect the learning experience and to address difficulties. Research suggests that listening to students, asking them appropriate questions, and giving them the opportunity to show what they know in a variety of ways are effective strategies that increase student learning.(10)

Students will be expected to:

• engage in regular reflection and self-assessment of their performance.

Actions to support this recommendation

Faculty actions:

• incorporate classroom assessment activities into class activities on a regular basis
• provide feedback at times and in ways that are most helpful to students
• adjust classroom activities in response to assessment information
• discuss assessment results with students and explain how the information is being used to make instructional decisions.

Departmental/Institutional actions:

• support faculty in their assessment efforts in the mathematics classroom
• provide professional development and training in assessment techniques for mathematics faculty
• provide support in and out of the mathematics classroom for implementation of recommendations based on assessment results.

Course Assessment

Course assessment extends class assessment by involving the department collectively.  This type of assessment, which begins by defining assessment terms and broadly communicating these definitions to mathematics faculty and the college community, remains fairly constant over time.  Mathematics faculty should first agree upon the core student learning outcomes for each mathematics course.  Course outcomes are the same for all sections of a given course, while individual instructors may include additional learning outcomes in class syllabi.  Courses taught using a variety of instructional modalities should use equivalent assessment tools to ensure student learning is occurring at a high level regardless of the method of instructional delivery.(11)  A focus on competencies is the bridge between using the traditional measure of class-time and using new and varied methods of instructional delivery as the determining factor to award credit hours.  When developing learning outcomes, attention must be given to reasoning skills and ways of thinking about and communicating mathematics, in addition to necessary learning outcomes about facts and procedures.

All course outcomes should be communicated to students in each section of the course at the beginning of the term.  Each instructor should refer to the outcomes as the term progresses so that students can evaluate their own learning relative to the stated course outcomes.  A course-based assessment may be administered at the end of a term by all faculty teaching the course. Other assessment formats may be equally effective.  Assessment instruments should directly measure student performance relative to one or more course learning outcomes.   

Data gathered from all course sections, or a representative sample, should be aggregated and analyzed.  Care must be taken to present assessment results without linking specific class section results to specific instructors.  Course assessment should be used to assess overall student learning of course outcomes, not to evaluate individual instructors.  Individual instructors should compare their students’ performance to that of the department to better understand the relationship between specific classroom materials and methods, and student learning.  Faculty in the mathematics department as a whole should reflect upon and discuss the assessment results, materials, and processes leading to those results. This important step in the course assessment process is where best practices are discussed and where improvements to a course are planned.

Data should also be disaggregated to compare results of diverse student subpopulations.  It is important to monitor the learning of various subpopulations and to consider any differences that occur in order to develop strategies to address the cause of any learning deficiencies.  Similarly, it may be useful to analyze the characteristics that distinguish the top quartile of learners from the lowest quartile.

If students as a group are not achieving the desired course outcomes, faculty should respond in one or more ways to implement the agreed upon changes and begin the cycle again.  This may include re-examining course content or prerequisites or assessment tools, altering teaching methods or activities, changing the type and frequency of testing, adjusting the percentage of group work or lecture, or modifying the amount of feedback or individual attention given to students.  Course assessment provides a systematic process to enact these improvements and a structure that encourages faculty to reflect upon and discuss what best helps students learn mathematics course content.

Students will be expected to:

• be aware of and focus their study on achieving learning outcomes.

Actions to support this recommendation

Faculty actions:

• agree upon the core student learning outcomes for each mathematics course
• communicate course outcomes to students at the beginning of each term.

Departmental actions:

• involve full-time and adjunct faculty in designing and implementing course-based assessment
• link department-wide assessment instruments to course outcomes
• assess courses using a representative group of students
• plan for and conduct periodic assessment of all mathematics course outcomes
• analyze assessment data and use the results to improve student learning.

Program Assessment

Assessment of student learning outcomes at the program level is an important complement to indirect assessments such as student retention and unit cost studies that are generally part of a program review.  Program assessment has three components: (1) assessment of mathematics programs; (2) assessment of other academic programs that include mathematics learning outcomes; and (3) assessment of the mathematics component of the college’s general education outcomes.

The first component of assessment of the mathematics program refers to the assessment of a sequence of mathematics courses.  For example, mathematics departments should assess the algebra sequence from pre-algebra through college algebra, the calculus sequence, and the sequence of mathematics courses required for business majors or prospective teachers.  The outcomes for all courses within the mathematics department should clearly illustrate the relationship among the various mathematics courses and what students should learn in each course.  Course outcomes in sequential or prerequisite courses should be designed so important concepts are learned well and unnecessary review is eliminated.  If the curriculum, the courses, and the process of learning are integrated, gaps in students’ learning are minimized.(12)  Assessment of student learning in developmental mathematics is especially important because those courses are prerequisites to many other courses.  Assessment in the developmental mathematics program should measure the quantitative literacy and other mathematics skills necessary for student success in future college-level courses. 

The second component in program assessment involves assessing mathematics outcomes in non-mathematics courses and programs.  Since student success in many academic programs is directly linked to student learning in mathematics, mathematics faculty should collaborate with faculty in other programs.  An analysis of results from the assessment of student learning at the end of such programs should be shared so faculty can collaborate to improve curriculum and instruction.  Just as outcomes must be aligned in sequences of mathematics courses, so must outcomes be aligned between prerequisite mathematics courses and courses in other disciplines to give students the best opportunity to achieve academic goals.  In this process, faculty may also discover that the mathematics content of a prerequisite course needs to be adjusted.

Mathematics faculty should also provide leadership for the third component of program assessment–the assessment of quantitative literacy at the college level.  Mathematics skills and processes, mathematical modeling, and problem solving should be taught across the curriculum.  If students are to be quantitatively literate, they must have opportunities to practice this in several contexts and in increasing sophistication throughout their learning experience. Data from program assessment may reveal that quantitative thinking is, in fact, not integrated across the curriculum, or that the problem-solving skills expected of our students upon graduation is different from the problem solving they practice while enrolled in classes. 

Assessment tools for program assessment may include portfolios containing examples of student work linked to specific program outcomes, tests administered in the final course in the sequence, or cross-sectional samples of student work collected in “key courses” taken by all students enrolled in the program. Rubrics are often developed to describe and scale levels of student achievement on specific performance tasks.(13)  An interdisciplinary capstone course or student electronic portfolios may be an effective means of assessing college-wide general education outcomes, providing a forum to identify gaps between desired and actual student learning, and showing students the connections between disciplines.

Program assessment requires that faculty work through the Assessment Implementation Cycle and seek reasons when students do not achieve desired mathematics outcomes.  It is important to implement the improvements, which may involve course alignment, changes in prerequisites, or increased mathematics requirements, and proceed through the cycle again.  Program assessment can also identify problems in structures, such as placement processes, that can serve as barriers to learning mathematics.  

Actions to support this recommendation

Faculty actions:

• identify assessment tools linked to desired student learning outcomes and proceed through the Assessment Implementation Cycle to implement improvements
• participate in the development and assessment of general education outcomes in mathematics
• determine which of the general education outcomes are met by completing a mathematics course.

Institutional actions:

• encourage collaboration among departments regarding instruction and assessment of mathematics outcomes embedded in non-mathematics courses
• implement periodic reviews and redesign of student learning outcomes in mathematics. 

Conclusion

Good assessment practices lead to faculty reflection and action to improve student learning in mathematics.  Assessment must occur at the class, course, and program levels of instruction and across different instructional and delivery models.  All assessment efforts must be linked to student learning outcomes and assessment tools must be designed to measure what faculty believe is important for students to learn.  When analyzing data, unfavorable results should be considered, as well as favorable results.  Realizing a problem exists (that students are not achieving an outcome) is the first step in motivating faculty to consider changes.  The most important result of assessment efforts is the discussion and introspection among mathematics faculty about what is really important for students to learn and how best to help them learn it. 

Assessment plays a key role in both the scholarship of teaching and learning and professional growth.  Educational assessment must be aligned not only with the design of thoughtful curricula and instructional strategies, but also with assessment practices that measure student learning relative to stated course and program outcomes. Assessment is integral to all that educators do and is important to the implementation of the principles and standards of Beyond Crossroads.