Beyond Crossroads Chapter 3

Chapter 3 The Implementation Standards of Beyond Crossroads

Beyond Crossroads extends the three sets of standards from Crossroads in Mathematics with an additional set of standards called Implementation Standards. The content of each of the following chapters focuses on one Implementation Standard.

Student Learning and the Learning Environment	Chapter 4
Assessment of Student Learning	Chapter 5
Curriculum and Program Development	Chapter 6
Instruction	Chapter 7
Professionalism	Chapter 8

Each section within a chapter presents research and rationale, expectations of students, recommendations, and action items for faculty, departments, and institutions for a particular issue in mathematics education in the first two years of college. The following Implementation Standards are guidelines for faculty, departments, and institutions for improving mathematics education in the first two years of college for all students–those underprepared in mathematics, as well as those ready to enter, or bypass, beginning calculus.

Implementation Standard: Student Learning and the Learning Environment

Mathematics faculty and their institutions will create an environment that optimizes the learning of mathematics for all students.

Two-year colleges serve a student body with varied characteristics and academic needs. Each student is entitled to the best educational experiences and opportunities available regardless of age, gender, sexual orientation, race and cultural differences, socio-economic factors, physical and cognitive abilities, or pre-college experiences. Creating a learning environment that maximizes student learning in mathematics and responds to the needs of all students requires the active involvement of every faculty member and each component of the institution.

Implementation Standard: Assessment of Student Learning

Mathematics faculty will use the results from the ongoing assessment of student learning of mathematics to improve curricula, materials, and teaching methods.

Assessment of student learning of mathematics should be aligned with curriculum and instruction to support student learning. Effective assessment practices include the documentation of student learning at the class, course, and program level.

Implementation Standard: Curriculum and Program Development

Mathematics departments will develop, implement, evaluate, assess, and revise courses,course sequences, and programs to help students attain a higher level of quantitative literacy and achieve their academic and career goals.

Mathematics departments, in collaboration with appropriate stakeholders, should regularly engage in course and program review and evaluation to assure that the mathematics curricula prepare students to be numerate citizens and productive employees who have an appreciation for mathematics and lifelong learning. These course and program reviews and the subsequent revisions should reflect the department’s own analysis of student achievement and the informed practice of the mathematics community.

Implementation Standard: Instruction

Mathematics faculty will use a variety of instructional strategies that reflect the results of research to enhance student learning.

Effective mathematics instruction requires a variety of resources, materials, technology, and delivery systems that take into account students’ different learning styles and instructors’ different teaching styles. Using multiple strategies in the classroom will increase the level of engagement of students and open opportunities for more students to be actively involved in the learning of mathematics.

Implementation Standard: Professionalism

Institutions will hire qualified mathematics faculty, and these faculty will engage in ongoing professional development and service.

Institutions should be proactive in recruiting candidates with diverse backgrounds and hiring qualified mathematics faculty. These faculty need to continually expand their mathematics knowledge, stay current with new research on learning and teaching, and be active in the college and the profession. The institution should support mathematics faculty by providing opportunities for faculty to learn and grow in their profession.

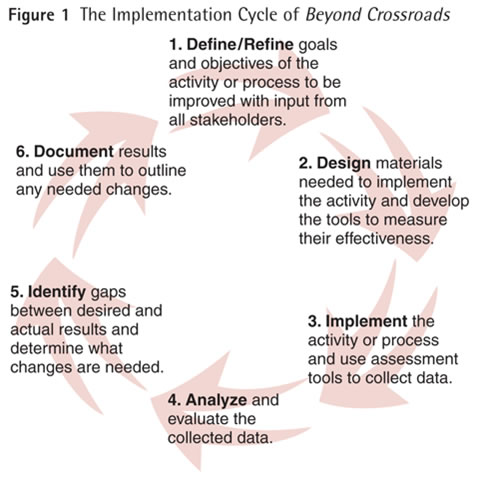
The Implementation Cycle of Beyond Crossroads

As a complement to the Implementation Standards, the following six-step Implementation Cycle is presented as a model for making change and improvements in a component of mathematics education. Mathematics professionals who find implementing standards somewhat overwhelming may find that the cycle provides a step-by-step process for continuous improvement. Embracing change with this model may be more comfortable in small, manageable steps. This cycle can be adapted to any standard, program, course, activity or process–from designing the optimal classroom, assessing student learning, designing curricula, choosing an instructional strategy, to hiring a new faculty member. Like Polya’s problem-solving method and other improvement models (i) , the steps of the model remain constant, with the specific activities within each step dictated by the particular situation being implemented, evaluated, and improved.

Inherent in the Implementation Cycle is assessment. Evaluative data is collected, analyzed, and used to refine goals and objectives. Then the cycle begins again. This feedback loop–implementing changes, refining goals, and beginning the cycle again–is perhaps the most important, and too often neglected, phase of the change cycle. What has been learned from implementation and assessment must be used to improve the activity the next time. The dynamic feedback loop should never end.

The Implementation Cycle

1. DEFINE and build consensus on goals and objectives of the activity or process to be implemented. Gather input from all stakeholders and advisory groups. Be sure to consider the current situation and specific aspects of the activity or process.

2. DESIGN (or obtain) the materials needed to implement the activity and develop the assessment tools and instruments to measure the achievement of goals and objectives. Identify and obtain needed equipment. Hire and train personnel.

3. IMPLEMENT the activity or process. Use the measurement tools to collect data.

4. ANALYZE and evaluate the collected data.

5. IDENTIFY gaps and determine what changes are needed. Investigate the degree to which desired goals and objectives are achieved. Determine the strengths and weaknesses of each component of the activity.

6. DOCUMENT results and use them to outline revisions in the activity or process. Agree on changes in the activities or measurement tools to meet desired goals when the activity is offered again.

Revisit step 1. REFINE goals and objectives of the activity or process. Request input from stakeholders regarding revisions in the activity and proceed through the cycle again. Implementing changes and beginning the cycle again, is perhaps the most important phase of the change cycle.

Periodic reviews and input from all stakeholders assure that curriculum and instruction are dynamic and the ever-changing needs of all students are addressed. To assess progress when using the Implementation Cycle, the following questions may be helpful.

	DEFINE	Have key issues been clearly defined? Have all stakeholders had an opportunity to provide input? Have goals, objectives, and outcomes of the activity or process been clearly defined? What can be learned from research about the activity?
DESIGN		What resources (equipment, personnel) are needed and are they available? Have all the necessary materials been developed (or obtained)? Have appropriate instruments been developed to assess the activity? Have personnel been hired and trained adequately for this task?
IMPLEMENT		Was the activity implemented according to the agreed upon plan? Was data collected to evaluate the outcomes?
ANALYZE		Has the collected data been analyzed and evaluated?
IDENTIFY		What was learned from the collected data? What were the strengths and weaknesses of the activity? What were the gaps between desired and actual outcomes? What changes are necessary to improve the activity?
DOCUMENT		Were the results of the evaluation used to outline revisions in the activity or program? Have the results of the evaluation been documented and communicated broadly to those involved?

The dynamic feedback loop, followed by outlining what has been learned from implementation and assessment to improve the activity the next time, is the key component to continuous improvement.

REFINE

Which goals, objectives, and/or activities need to be revised?
What changes are necessary to close the gaps between desired and actual outcomes?
Have stakeholders been consulted again regarding revised goals, objectives, and activities?

Begin the Cycle again

Implementing the Vision

Thoughtful implementation of the principles and standards presented in Beyond Crossroads is an ongoing process. The cooperative engagement of the Principles, the Intellectual Development, Content, and Pedagogy Standards, and the Implementation Standards is synergistic. Implementing a group of standards in concert has a greater effect on the improvement of student learning and the professionalism of faculty than any single standard implemented in isolation. Beyond Crossroads presents research about the learning and teaching of mathematics and guidance on how to implement new strategies and argues for an action-oriented vision. The standards-based mathematics education addressed in this document is intended to guide professionals in their decision-making and provide a forum for dialogue on how to design strategies to meet the challenges of improving student learning in mathematics. The goal is to empower faculty to strengthen the learning and teaching of mathematics by creating changes based on informed decision-making and goals and objectives defined with input from all stakeholders. The Implementation Standards presented in the following chapters address that implementation process.