Assessment Electronic Resources

 

Implementation Standard: Assessment of Student Learning Mathematics faculty will use results from the ongoing assessment of student learning of mathematics to improve curriculum, materials, and teaching methods.

 

Chapter 5 of Beyond Crossroads discusses the assessment of student learning. The menu items to the right allow you to view links to websites, videos and other electronic resources regarding assessment at the class, course and program level.

 

Assessment at Three Levels

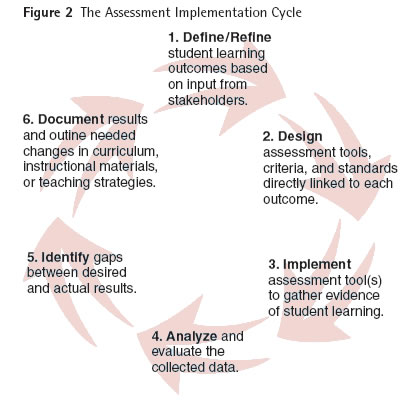The assessment cycle provides assurances to students, colleagues, and the external community about the content and quality of mathematics in the first two years of college. Effective assessment includes the documentation of student learning at three levels: class, course, and program. Assessment at each level is the responsibility of all faculty.  It should reflect not only student knowledge of facts and procedures, but also critical thinking and ways of thinking about and communicating mathematics.  When faculty begin an assessment, they should start on a small scale, choosing one or more course or program outcomes to assess.  As faculty gain facility with the assessment process, other learning outcomes can be added to the assessment plan. 

Classroom assessment involves individual instructors assessing individual students’ learning outcomes with instructor-developed tools.  Many assessments are used throughout the term and changed frequently.  Students are informed often about their progress.  Individual faculty who use classroom assessment techniques discover how to adapt instruction to address the learning needs of individual students in a specific mathematics class.  Faculty make frequent and immediate changes to class activities and methods based on assessment results.

 

Assessment efforts at the course level provide evidence of student learning and motivate changes beyond the individual classroom.  Learning outcomes in individual mathematics classes, in all sections of a particular course, or in sequences of courses or specific programs, are assessed to determine if students are meeting agreed-upon course learning outcomes.  A group of faculty teaching intermediate algebra, for example, can collaborate to discover the instructional strategies or materials best suited to help all students learn the relationship between a quadratic equation and its corresponding graph, an agreed-upon course outcome. 

Assessing outcomes at the program level is the broadest and most overarching form of assessment discussed in this chapter.  Faculty should develop a consensus about the essential student learning outcomes for mathematics courses and programs, as well as the college’s quantitative literacy general education outcomes.  Faculty can use the results of program assessment to determine how all courses in a program, mathematics and nonmathematics courses, help students achieve quantitative goals and objectives.  In addition, external accrediting agencies may have an impact on mathematics outcomes within programs. 

Although classroom assessment should be ongoing, course and program outcomes may be assessed at regular intervals with faculty choosing a different course or program each year.  It is important, however, to complete the assessment cycle for the learning outcomes chosen. In addition to collecting data about many outcomes, improvements should be implemented based on an analysis of that data. 

 

This material is based upon work supported by the National Science Foundation under Grant No. 0410842. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.