Chapter 6

Curriculum and Program Development

            Although mathematical truths may be timeless, the content of mathematics programs and courses continues to evolve, often as a result of rapid technological advances.  This chapter focuses on the improvement of student learning in mathematics by developing, assessing, and improving mathematics courses and programs.  The intent is not to prescribe specific mathematics course content, but rather to emphasize key components of curricular design and development and encourage periodic review and revision of curricula with the goal of continuous improvement. 

The Changing Curriculum

Creating a responsive learning environment, assessing student learning, and improving student learning in mathematics requires a dynamic curriculum.  There are a number of factors that influence the content and organization of the mathematics curriculum.

• Advances in technology influence both how mathematics is taught and what mathematics is taught. For example, the square root algorithm and trigonometric tables are rarely used today, whereas spreadsheets and graphing technology are widely used. 
• Educational research provides information about how students learn mathematics.  These findings should influence how mathematics is taught and how the curriculum is designed.  For example, a well-developed understanding of functions facilitates the transition to advanced mathematical thinking.(1)
• The mathematics needed for successful careers and responsible citizenship continues to change.  To be productive, citizens need to be quantitatively literate.  For example, individuals are bombarded with information, in their daily lives and in their jobs.  To make informed decisions and understand issues, citizens must be able to analyze data, reason with statistics , and understand mathematical models. 
• The global economy has changed people’s lives and the workplace. The number of unskilled labor positions and jobs that require repetitive processes is decreasing.  Conversely, the need for employees who are innovative, can use technology, and are able to think critically is increasing.  For example, many processes are now automated, replacing production workers.  However, the need for trained technicians who can understand those automations and repair them continues to increase.
• A decrease in the number of students choosing science, technology, engineering, or mathematics as a major, as well as a shortage of instructors in these areas, is affecting the nation’s ability to compete in this global economy.  In order to find competent employees at lesser salaries, many corporations have established technical support services based abroad.

In response to these factors, faculty need to take the lead in careful, deliberate, informed curricular revision decisions.  Research in mathematics education can provide helpful information to guide decision-making in curricular design.  The challenge is to design curricula that address the needs of as many academic paths and disciplines as possible.  To meet the diverse needs of all students mathematics departments need to collaborate with others (faculty in other disciplines, faculty in four-year institutions, business and industry representatives) to determine appropriate mathematics outcomes.  Once the outcomes are established, faculty must access the degree to which students meet those outcomes.

During the last decade, several key curricular issues have stimulated dialogue and educational research. For example, since 1989, when it was suggested that “If it does nothing else, undergraduate mathematics should help students develop function sense…,”(2) considerable research has been conducted on what it means for students to have an understanding of function.  Studies report that a well-developed understanding of function correlates closely with success in calculus, as well as facilitating the transition to advanced mathematical thinking.(3)  In addition, faculty continue to search for methods to develop a student’s understanding of the concept of variable.  Students who are able to view variables as representing quantities whose values change dynamically along a continuum have been shown to have ready access to fundamental ideas, such as rate of change and limits, and exhibit higher levels of achievement in mathematics.(4) 

There have also been lively discussions about what is the appropriate content of General Education Mathematics, College Algebra, and Precalculus.  For example, do students need to analyze data and construct appropriate models of real-world phenomena?  If so, then curricula need to be designed so that students understand the difference between a constant rate of change (additive, linear) and a constant growth factor (multiplicative, exponential). While learning to distinguish between the two processes, students develop fluency in pattern recognition, data analysis and proportional reasoning. (5)  These discussions, within a department, institution, or professional organization are valuable professional development opportunities for all.  Faculty and departments are encouraged to continue discussions, consult mathematics education research, and consider educational innovations when designing a curriculum.

The goal and challenge for faculty is to create courses and programs that empower students to become confident and competent problem solvers.  Courses should provide opportunities to develop the quantitative skills they will need in their academic work, in society, and in the workplace.  The dynamic nature of the curriculum requires a continuous re-examination of how, what, and when mathematics content is taught.  The focus of curricular development should be on the mathematics content that is most appropriate for student learning. 

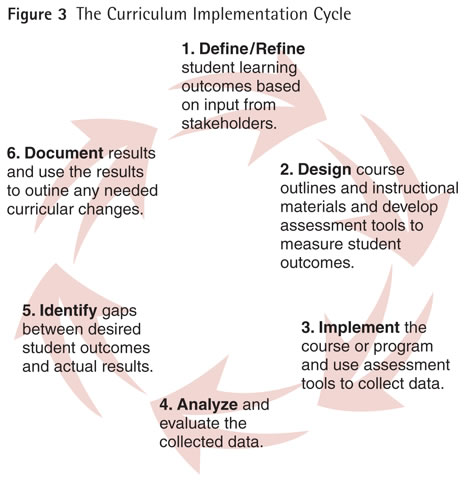
The Beyond Crossroads Implementation Cycle can be applied to curriculum development, outlining a process for identifying goals, assessing strengths and weaknesses, and implementing curricular change as shown in Figure 3.

Quantitative Literacy

The use of quantitative ideas and language is pervasive in society, news stories, scientific reports, and advertising.  Because information is often presented in a variety of representations–words, symbols, tables, or graphs–individuals need to be able to interpret, analyze, and draw conclusions about information presented in these forms. It is important that all citizens have an understanding of the magnitude of numbers, be able to compute and apply percentages, and apply the basic concepts of statistics.  In order to be informed consumers, to interpret economic and political trends, or to evaluate health risks of new drugs or treatments, individuals need to understand basic concepts of proportionality, linear and exponential growth, and elementary descriptive and inferential statistics.  While entry level jobs may not require significant quantitative reasoning, higher levels of quantitative literacy may be needed to keep open the doors to job advancement.   

For these reasons, quantitative literacy should be an outcome of all programs within the college.  While most professionals agree on the need for quantitative literacy for all students, there are variations in terminology and definition.  Quantitative literacy, quantitative reasoning, numeracy, and mathematics across the curriculum all share many common components. Definitions of quantitative literacy outline student outcomes that range from acquiring specific mathematical skills to gaining mathematical confidence.  Quantitative literacy may include the following:

• The ability to apply aspects of mathematics (including arithmetic, measurement, data representation, number sense, variables, geometric shapes, spatial visualization, and chance) to understand, predict, and control routine events in people’s lives;(6) the ability to apply arithmetic operations, either alone or sequentially, in many contexts including balancing a checkbook and completing tax forms.(7) 
• Statistical reasoning skills and the comfort and confidence to deal with fundamental quantitative problems using critical thinking and problem-solving skills. 
• Knowledge of the power and utility of mathematics and how it has shaped civilization.(8)

Acknowledging that more than one definition exists, Beyond Crossroads accepts the definition of quantitative literacy presented in the basic principle for quantitative literacy in Chapter 2: an individual’s “capacity to identify, understand and engage in mathematics as well as make well-founded mathematical judgments as a constructive, concerned and reflective citizen.”(9)  Quantitative literacy includes “five different dimensions of numeracy:  practical, for immediate use in the routine tasks of life; civic, to understand major public policy issues; professional, to provide skills necessary for employment; recreational, to appreciate and understand games, sports, and lotteries; and cultural, as part of the tapestry of civilization.”(10)  While the specific definitions may vary, quantitative literacy is an important general education outcome for every college student.  Thus, quantitative literacy outcomes should be woven into every mathematics course and as many other college courses as possible.

Quantitative literacy is more about habits of mind than specific mathematical content.  Therefore, the responsibility for developing quantitative literacy, like writing across the curriculum, is shared by the entire college faculty.  However, mathematics faculty should lead the quantitative literacy movement by helping to establish a set of outcomes expected of students in each program.  There are some outcomes expected of all students.

Students in all college programs will be expected to:

• exhibit perseverance, ability, and confidence to use mathematics to solve problems
• perform mental arithmetic and use proportional reasoning
• estimate and check answers to problems and determine the reasonableness of results
• use geometric concepts and representations in solving problems
• collect, organize, analyze data, and interpret various representations of data, including graphs and tables
• use a variety of problem-solving strategies and exhibit logical thinking
• use basic descriptive statistics
• utilize linear, exponential, and other non-linear models as appropriate
• communicate findings both in writing and orally using appropriate mathematical language and symbolism with supporting data and graphs
• work effectively with others to solve problems
• demonstrate an understanding and an appreciation of the positive role of mathematics in their lives.

Actions to support this recommendation

Faculty and Departmental actions:

• determine appropriate quantitative literacy outcomes for each mathematics course and include these outcomes in course outlines
• assume a leadership role in experimenting with new instructional materials to develop quantitative literacy and evaluating and sharing the results
• promote mathematics across the curriculum and positive attitudes by all faculty and students towards mathematics
• initiate collaborations with faculty from other disciplines to promote the integration of quantitative literacy in all programs at the college
• discuss course content and uses of technology in the mathematical sciences.

Institutional actions:

• promote general education outcomes that include quantitative literacy
• provide opportunities for continuing conversations throughout the college on student outcomes in quantitative literacy
• support faculty from all disciplines in developing and implementing courses that integrate quantitative literacy.

Developmental Mathematics Courses and Programs

Developmental mathematics courses in this document are defined to be courses below the level of the first mathematics course that earns full college credit at the institution.  For most two-year colleges, this includes mathematics courses below the level of intermediate or college Algebra. 

Developmental mathematics courses, to a greater extent than other mathematics courses, serve students with various degrees of success in previous mathematics courses.  Appropriate student placement is crucial for developing positive attitudes and maximizing success.  The goals of a solid preparation in basic mathematics and swift progress through the curriculum can be compatible.  Substantial changes to traditional developmental mathematics curricula, which were derived primarily from high school curricula, need to be implemented.  The developmental mathematics program needs to be designed to accomplish agreed-upon goals designed with input from stakeholders, using instructional strategies appropriate for diverse student learning styles and diverse teaching styles.  In order to help students who have not previously been successful in mathematics and to implement the recommendations in this report, faculty need to do more than teach the same mathematics again.

The desired student outcomes for developmental mathematics courses should be developed in cooperation with the partner disciplines.  The content for these courses also should address mathematics anxiety, develop study and workplace skills, promote basic quantitative literacy, and create active problem-solvers.  The curriculum of developmental mathematics programs should:

• develop mathematical knowledge and skills so students can successfully pursue their career goals, consider other career goals, and function as successful citizens
• develop students’ study skills and workplace skills to enable them to be successful in other courses and in their careers
• help students progress through their chosen curriculum as quickly as possible.

Teaching a developmental mathematics course presents unique challenges.  Each instructor needs to provide a positive, nurturing experience for each student.  Students need to develop time management skills and study habits.  They should engage in activities to help them view mathematics as interrelated concepts of a formal system, not just as unrelated facts to be memorized.  While students need skills such as solving proportions, they also need to understand the concept of proportion and recognize its application in their lives and careers.  Students should be able to approach mathematics through contextual, concrete, and abstract situations; apply mathematical skills to solve problems; and be able to transfer their knowledge to new situations. Students should experience multi-step problems and be comfortable working in groups and doing collaborative projects.  They also should have successful experiences using technology, including calculators, spreadsheets, and other computer software, as a tool to collect, organize, and analyze data, as well as to recognize numerical and graphical patterns. 

Topics in developmental mathematics courses should be taught in depth and not as a preview of topics to come in later courses.  For many students, any given mathematics course could be their last one.  Some algebraic topics, such as factoring, radicals, and operations with rational expressions, should receive less attention, while modeling, communication, and quantitative literacy and reasoning should receive more attention.  Topics in algebra, geometry, statistics, problem solving and experience using technology should be integrated throughout developmental courses.  However, students should still be expected to perform single digit arithmetic, without the use of a calculator.   In addition to the quantitative literacy outcomes and workplace skills expected of all students, there are some global outcomes that are expected of all developmental mathematics students.

Developmental mathematics students will be expected to:

• apply strategies to manage mathematics anxiety
• develop mathematical skills needed to complete other courses successfully
• gain confidence in doing mathematics and solving real-world problems.

Actions to support this recommendation

Faculty actions:

• design courses and classes to produce desired student outcomes in developmental mathematics
• be actively involved in student placement to ensure each student is placed appropriately
• be sensitive to the impact of mathematics anxiety on students and employ strategies to control, manage, and reduce student anxiety
• provide opportunities to develop student confidence in mathematics and problem solving
• demonstrate and encourage multiple problem-solving strategies using appropriate tools from algebra, geometry, and statistics
• seek ways to integrate technology into developmental mathematics courses as a tool to investigate and promote understanding of mathematical concepts.

Departmental actions:

• create developmental mathematics courses and programs for students who only need to refresh their knowledge of basic concepts
• create developmental mathematics courses and programs for students who are taking developmental mathematics for the first time
• collaborate with faculty from other disciplines to ensure the student outcomes for developmental mathematics courses are appropriate.

Institutional actions:

• provide appropriate student support services for mathematics students
• provide professional development for mathematics faculty focusing on teaching developmental mathematics.

General Education Mathematics Courses

For many students, a general education course such as logic, statistics, liberal arts mathematics, finite mathematics, or discrete mathematics may be the only mathematics course required for graduation.  A general education mathematics course may not be a prerequisite to any subsequent course, but a prelude to the student’s experiences as a productive employee and informed, quantitatively literate citizen.  As a result, it is critical that general education mathematics courses exemplify the principles and standards of this document.   A general education mathematics course may mold students’ opinions of mathematics for the rest of their lives.  These courses should pay particular attention to influencing positively student attitudes toward mathematics.

General education courses should include the important general education outcomes of writing, critical thinking, and quantitative literacy. While the course goals and student outcomes may vary from program to program, all general education courses in mathematics should require students to synthesize, make connections, and use basic mathematical knowledge to solve real-world problems.  This synthesis may occur in a variety of mathematical contexts through exploration, discovery, and problem solving.  A course may be designed to focus on mathematics as a language used to describe relationships and patterns.  Another course might examine how one quantity varies with another (especially in linear, quadratic, and exponential relationships using real data) through a study of functions, geometric patterns, or statistics.  Many kinds of investigations, such as using real data, integrating algebraic or geometric structures, or studying statistics, could be used as the core of a general education mathematics course. 

In addition to the quantitative literacy outcomes expected of all students, the following are expectations of general education students.

General education mathematics students will be expected to:

• use mathematics and technology to investigate, model, and solve a variety of real-world problems
• use a variety of problem-solving methods
• use mathematics to write and communicate in their discipline
• view mathematics as a language to describe relationships and patterns
• synthesize their mathematical knowledge.

Implementation recommendation:Mathematics departments will design and offer general education mathematics courses for students who take a single college-level mathematics course in their college degree program.

Actions to support this recommendation

Faculty actions:

• collaborate with faculty from other disciplines to determine learning outcomes for general education mathematics courses
• develop and offer mathematics courses to meet general education requirements that model basic principles and standards of this document
• demonstrate the use of technology to find patterns, test conjectures, and discover properties.

Technical and Career Courses and Programs

Mathematics courses in technical programs include topics from arithmetic through calculus. In addition to providing necessary mathematical skills, these mathematics courses should build students’ quantitative literacy, develop their ability to think and communicate mathematically, connect mathematics to real-world situations, and develop problem-solving skills for working alone, as well as for working in teams.(11)

Colleges offering technical and career programs have the responsibility of determining the needs of their local businesses and industries and preparing students to meet these needs.  Employers value thinking skills, decision-making, creativity, problem-solving, visualizing and reasoning spatially, and knowing how to learn–as well as personal qualities such as responsibility, self-management, and team skills.  Employers need college graduates with reading, writing, speaking, and listening skills, as well as knowledge of basic mathematical concepts.(12)  Designing technical courses with mathematics content for specific fields, with flexibility to be used by more than one major, is another challenge.  For example, emerging technologies, such as those in the biotechnological fields, tend to require fewer algebraic skills, and more data analysis, modeling, statistics, and discrete mathematics.

Technical mathematics courses and programs should be developed in collaboration with faculty from other disciplines and business and industry representatives to identify and address the mathematics content needs of specific program employers.  Content in two-year technical mathematics courses should be selected because of its application to a specific technical field and the needs of specific employers. It should be at a level equivalent to mathematics courses that transfer to four-year institutions.  The direction of curriculum change in technical and career programs is to emphasize workplace skills within the classroom context and to develop flexible thinkers who can work collaboratively to solve new problems. In addition to quantitative literacy outcomes, technical and career students have unique expectations from their respective programs.

Technical and career students will be expected to:

• develop the mathematical concepts necessary to succeed in their chosen program
• use technology to explore and analyze problems
• analyze and model data from their career fields and use these models to solve problems
• be able to use mathematics to communicate orally and in writing
• develop workplace skills including collaborative problem-solving skills. 

Actions to support this recommendation

Faculty actions:

• consult with representatives from business, industry, and technical disciplines and use their input to keep course content relevant
• incorporate workplace skills as an integral part of the curricula
• encourage active student learning and the development of team-building skills with term projects, collaborative projects, portfolios, research, field investigations, or internships
• use technology throughout curricula to discover properties, to develop concepts, and to examine multiple perspectives
• give students experience with the technology skills they will use routinely in the workplace.

Departmental and Institutional actions:

• provide professional development for faculty that focuses on technical and career mathematics courses and programs
• provide support for faculty in seeking outside funding to support the technology appropriate for the curriculum.

Teacher Preparation Courses and Programs

Many two-year colleges have the preparation of teachers as part of their mission.(13)  Many future teachers take most, if not all, of their college-level science and mathematics courses at two-year colleges.  Two-year colleges enroll a large proportion of the nation’s underrepresented groups and can assume a key role in recruiting minorities to the teaching profession.  Positioned between K-12 schools and four-year colleges, two-year colleges can play an important role in promoting collaboration in a variety of issues, such as articulation and transfer issues, curriculum development, financial support for students, use of technology, program requirements, statewide teacher licensure requirements, and professional assessments.(14)  Because of these factors, two-year colleges play a pivotal role in the recruitment and preparation of teachers. 

To be effective teachers of mathematics, “Prospective teachers need mathematics courses that develop a deep understanding of the mathematics they will teach.”(15)  Courses for prospective teachers should develop the habits of mind of mathematical thinkers and demonstrate flexible, interactive teaching styles.  They should demonstrate the role of technology to explore ideas and promote concept development.  They also should present the fundamental ideas of school mathematics and be taught by mathematicians who have a serious interest in teacher education.  All mathematics courses taken by future teachers of mathematics should be standards-based, use strategies that have demonstrated success for students, and incorporate the NCTM’s Principles and Standards for School Mathematics.(16) 

Some of the courses taught at two-year colleges for prospective teachers of mathematics are addressed in the report The Mathematical Education of Teachers. (17) This report includes the following recommendations to mathematics departments regarding both the content and delivery of the curriculum.

• Prospective elementary grade teachers will take at least nine semester hours on the fundamental ideas of elementary school mathematics.
• Prospective middle school mathematics teachers will receive training designed specifically for future middle school teachers, which includes at least twenty-one semester hours of mathematics, including at least twelve semester hours on fundamental ideas of school mathematics appropriate for middle grades teachers.
• Prospective high school teachers of mathematics will complete the equivalent of an undergraduate major in mathematics, including a six-semester hour capstone course connecting their college mathematics courses with the high school mathematics curriculum.

Mathematics courses must emphasize the connections within mathematics, especially connections with the mathematics that is already familiar to the students.  The courses also should illustrate the connection between mathematics and other disciplines.  Mathematics instruction for future teachers should model informed teaching practices.  These practices include setting high expectations for all students, integrating concepts, actively engaging students in the learning process, emphasizing problem solving and reasoning mathematically, and expecting students to reflect on their learning and to communicate mathematically. 

Prospective teachers should have intensive courses in effective teaching methods in mathematics.(18)  Included in these courses should be a discussion of interactions between the learner and the instructor, among learners, and between learners and the content they are trying to master.  Whole group, small group, and individual work should be utilized. Instructors should integrate assessment into instruction and use multiple assessment techniques. 

Teachers tend to teach the way they were taught and many school children are concrete learners.  Therefore, future teachers–especially future elementary teachers–need pre-service experience using manipulatives as a tool to teach mathematics.  Manipulatives help develop conceptual understanding and assist students in discovering underlying procedures.  Future teachers need experience using the same manipulatives they will encounter in preK-12 classrooms.  They also need to practice with using the Internet, spreadsheets, mathematics applets, and mathematics software, as tools to teach mathematics.(19)

In the first two years of college, prospective teachers need supervised experiences in classrooms to observe and practice what they are learning in their mathematics courses.  These early experiences help students determine whether teaching is the right career choice for them.  Fieldwork experiences prior to student teaching afford students the opportunity to begin to become reflective practitioners and evolve in their understanding of educational practices and issues as they analyze, synthesize, and summarize their experiences.  Mathematics departments should coordinate with other disciplines to afford prospective teachers the opportunity to participate in early fieldwork experiences.

In addition to providing the first two years of a college-level teacher preparation program, many two-year colleges also offer a variety of other education-related programs.  Examples include degree programs in paraprofessional education and early childhood development, professional development workshops and licensure renewal courses for teachers, and teacher licensure programs for professionals holding bachelor’s degrees who desire to switch their careers.  In some states, colleges formerly considered two-year colleges are now granting bachelor’s degrees in high-need disciplines, such as mathematics or science teaching and health care. Recommendations about the mathematical preparation of future teachers also apply to those enrolled in other education-related courses and programs at two-year colleges. The expectations of future teachers extend beyond the quantitative literacy outcomes and workplace skills outlined earlier.

Students in teacher preparation programs will be expected to:

• develop a deep understanding of the mathematics they will teach and of the teaching practices that result in students' learning of mathematics
• include the manipulatives and technology used in preK-12 mathematics classrooms appropriately when designing lesson plans
• communicate mathematical concepts clearly both verbally and in writing
• clarify their career goals through supervised field experiences.

Actions to support this recommendation

Faculty actions:

• model the appropriate use of manipulatives and technology
• use multiple assessment strategies to assess students
• include supervised field experiences for future teachers in some of the mathematics courses
• recruit students from underrepresented groups into the mathematics teaching profession.

Departmental and Institutional actions:

• hire faculty with strong mathematics and education backgrounds to teach in teacher preparation programs
• place teacher preparation as a high priority in the department and have these courses taught by faculty members who have teacher education as one of their primary interests
• provide opportunities for professional development field experiences in collaboration with area four-year institutions and school districts
• work with four-year institutions and state departments of education to develop post-baccalaureate teacher licensure programs.
  

Mathematics-Intensive Courses and Programs

Mathematics-intensive programs serve students who will major in mathematics or mathematics-dependent fields, including secondary mathematics education, business, computer science, engineering, and science.  The demand for a mathematically educated workforce has grown, but the number of students majoring in mathematics has declined.  It is essential that students, especially those from underrepresented groups, be provided with a supportive learning environment that encourages their enrollment and retention in mathematics-intensive programs.

A solid understanding of functions and proof is a critical component of students’ mathematical foundation. Each student needs to develop an ability to work at an abstract level.  Students should use rich applications from various disciplines to deepen their appreciation and understanding of the power of mathematics to model real-world phenomena.  These applications can be used to promote active and collaborative learning, practice sustained effort, examine a variety of problem solving techniques, and communicate mathematically by giving written or oral reports. Mathematics-intensive programs should increase students’ understanding of the mathematics topics studied in calculus.  The expectations of mathematics-intensive students extend well beyond the quantitative literacy outcomes expected of all students.

Mathematics-intensive students will be expected to:

• develop an appreciation of mathematics as a whole and of the historical development of mathematics
• develop a solid understanding of functions from multiple perspectives
• be able to use numerical, graphical, symbolic, and verbal representations to solve problems and communicate with others
• use technology as a tool for exploring mathematical concepts
• use a variety of mathematical models including curve fitting
• develop an ability to work with mathematical abstractions, analyze mathematical relationships, make plausible conjectures, projections, and develop proofs
• develop an understanding of concepts and skills needed for future mathematics courses or courses in related disciplines.

Actions to support this recommendation

Faculty actions:

• create courses and activities to promote students’ ability to use multiple approaches or representations to examine mathematical concepts so that students develop a better understanding of connections among topics and improve their ability to work abstractly
• require group projects, group discussions, and explorations to promote the ability of students to use mathematical notation and terminology
• expect students to communicate orally and with written reports
• use technology to promote student discovery, develop concepts, examine multiple perspectives, and give students experience with the technology skills that they will use in their careers
• work with instructors in other disciplines to develop learning communities that pair a mathematics class with a class in another department
• provide guest speakers from scientific fields for student mathematics clubs or for selected classes
• encourage student participation in professional organizations through activities such as the AMATYC Student Math League, MAA Student chapters, and Mu Alpha Theta mathematics organizations
• recruit students, including those from underrepresented groups, into mathematics-intensive programs and careers.

Conclusion

Mathematics courses and programs in the first two years of college need to develop students’ quantitative and workplace skills and actively engage them in the mathematics they will encounter outside the classroom.  Faculty may need to teach content that is different from what they were taught, teach more than they were taught, and teach differently than the way they were taught.  Students should understand some of the big ideas of mathematics through a curriculum, a variety of problem-solving strategies, and significant projects that examine selected topics in depth.  Students should have opportunities to demonstrate their mathematical knowledge, as well as their creativity.  When designing mathematics curricula, faculty and departments should consider the needs of each student, as well as the mathematical requirements of other courses and the workplace, and employ multiple approaches in instructional strategies.  In addition, each course and program should be reviewed periodically for continuous improvement. The entire mathematics community needs to embrace continuous improvement as the process that can increase student learning.